intersection of two lines parametric equations

Find the parametric equations for the line of intersection of the.
The parametric equations of a line passing through two points. The direction of. Intersection point of a line and a plane in three dimensional space. The point of.
The xy-plane is z = 0. The directional vector v, of the line of intersection is orthogonal to the normal vectors n1 and n2 of the two planes. Take the.

intersection of two lines parametric equations

Simple but Stuck: How do I find the point of intersection of two lines.

(I assume you mean 2x-3y=4 for the second plane.) To find the line of intersection : Solve the simultaneous equations x+0y+2z=0 2x-3y+0z=4.

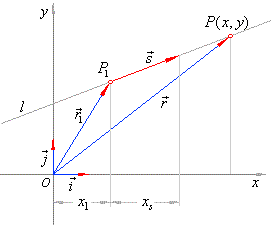
Math Basics - Line Equation.

Parametric equations use, Intersection point of line and plane - Nabla.
Intersections of Lines, Segments and Planes (2D & 3D).
Find a parametric equation for the line of intersection of the two.

(I assume you mean 2x-3y=4 for the second plane.) To find the line of intersection : Solve the simultaneous equations x+0y+2z=0 2x-3y+0z=4.
Parametric form of line equation in 2 dimension; Point-slope form of the line equation; Point-intercept of the line equation. Equations of Lines in 3 dimensions.
In any dimension, the parametric equation of a line defined by two points P0. When true, the two associated lines are either coincident or do not intersect at all.

intersection of two lines parametric equations

Parametric equation of the line of intersection of two planes.

Since the line is contained in both planes, it must be perpendicular to the normal of both the planes. This direction is given by the cross product of.
First, let's find the equation of the line of intersection of the two given. To get the parametric equations of the line just break up the vector.
Below is an example of this type of problem: Exercise: Determine the line of intersection of the following two planes. Write the parametric equations for this line.
(716, #15) Determine whether the lines and are parallel, skew, or.